Let's review the basic summation rules and sigma notation to find the limit of a sum as n approaches infinity. First let's review the basic rules and then we'll get to the problem - which is a problem you'd generally see preceding a discussion of the definite integral.
Recall that the "n" on top of the Sigma (the funny looking e) is the terminal value for the index which is located under the sigma. Note that the i= "something" tells you where to begin the summation.
1) Rule one states that if you're summing a constant from i=1 to n, the sum is equal to the constant multiplied by n. This makes intuitive sense. If i=1, and n = 100, and C was 1, 1(100) = 100.
2) Rule two states that the sum of increasing integers is simply n(n+1)/2. We'll leave the proof for another time but for now we can have faith in its utility.
3) Rule 3 states that the sum of increasing squared integers is equal to the formula.
4) Rule 4 is the same as rule 3 but handles the sum of increasing cubed integers.
Now let's evaluate the limit of a summation as n approaches infinity. Here's the problem: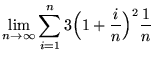
One of the first considerations we need to make is what isn't affected by i, or what term(s) doesn't need a summation rule to be applied to it? First let's collect all terms outside of the parentheses and then square the inside term. After we've set this up we can apply the summation formula to all the terms inside the parentheses. Here are the steps.
Now we have to evaluate each term. We know from rule 1 above, the sum of a constant is simply c*n. So this will just be n. The middle term will be 2/n* the rule above which handles the sum of increasing integers n(n+1)2. The third term is a bit tricker - we take a 1/n^2 and place it to the left of the Sigma and evaluate i^2, whose rule is listed above. Here's the result visually: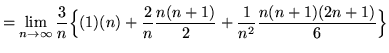
Now we'll simplify through algebraic manipulation and distribute in the 3/n.
So, as n approaches infinity the limit = 6 +1 = 7.
Keep in mind that when you're taking a limit as something approaches infinity - if the power of that something in the denominator is greater than the power of that something appearing in the denominator the term approaches zero as that something becomes large. After the 6, the 3/n is really 3/infinity which is zero as n becomes large. If you won 3 bucks and your friend won 3 billion you'd think very little of your winnings!
Not too bad - just remember to only apply the summation rules to terms that are impacted by them, namely i, or any expression involving i.
Sunday, April 6, 2008
Sigma Notation Summation Rules & Limits at Infinity
Professional Calculus 1 and 2 Study DVDs.
Subscribe to:
Post Comments (Atom)



9 comments:
thx, i just needed that for my AP Calc, respect! ;F
Hi whats the limit of summation of x^2 for x=0 to infinity?
Hi whats the limit of summation of x^2 for x=0 to infinity?
Infinity
What is the value of summation n.n!
what if there is no limit
It just the term for n=k+1
What is the limit of summation of i^5 for x=0 to infinity?
This is false. This is Riemann's sum, and is equal to integral from 1 to 2 xdx times 3.
Answer is: 4.5 !!!
Post a Comment