Differentiate Using Chain Rule Twice

Today we'll do a simple problem. Plain old differentiation using the chain rule but we'll have to apply it multiple times. Here's the problem: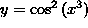

$tex2html_wrap_inline750$
Cos(x^3)^2 written differently. Keep in mind this isn't a product and we can't employ the product rule here. If you'd like to review the product rule however there's a link to a short video tutorial on the product rule at the end of this entry.

Recall that the chain rule is as follows:

$(f \circ g)'(x) = f'(g(x)) g'(x),\,$

In this case our f(x) is cos^2(x) and our g(x) is x^3. Let's begin to differentiate:

2*cos(x^3)*-sin(x^3)*3x^2 - here's the image of what I've written to the left -

$tex2html_wrap_inline768$ Let's think about this - we used the power rule to get the exponent in front of the cos(x)

$\frac{d}{dx} x^n = nx^{n-1}.$ power rule

Then you multiply the 2 by the inside of the balance of the functions. Then you take the derivative of the cos, which yields -sin, followed by the derivative of x cubed by itself. The final answer is a product of each successive differentiation.

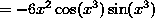$tex2html_wrap_inline770$ .
So remember - when using the chain rule more than once remember to keep differentiating the outer part of the expression and work your way inward, multiplying by the results of your differentiation to arrive at the final answer.

Here's a good video on the product rule - remember that the quotient rule is just the product rule in disguise and sometimes it's better to take a quotient and create a product through use of a negative exponent.