Integration By Parts - this is a method for solving integrals involving products of functions. By products of functions we mean:
f(x)g(x), or xCos[x], where x is a function and Cos[x] is a function. Here is the parts formula:
f(x) = x^2
f '(x) = 2x
Integral of 2x = (2 *x^2)/2, and the 2s cancel leaving us with x^2 or f(x).
So, since the left and right side of any equation are equivalent :-), we can also integrate the right side of the equation. After recalling the fact above, that the derivative of an integral is just the function and a little rearranging we arrive at the integration by parts formula. Look at the below.
- First is the product rule
- Then you integrate the derivative to get back the original f(x)*g(x) function.
- Then you rearrange the equation...that's it.
(note, in the first line, that's g ' (x), ignore the carrot, there is no exponent)
Let's do a integration by parts problem:

Notice here, U substitution doesn’t work. There’s no trig substitution to fall back on and there is no immediately obvious antiderivative.
Let’s use integration by parts, note, we will be replacing f and g with u and v, don’t get too excited!

-
-
So how do you choose u and v? Good question, let’s think about it for a second. Looking at the integration by parts formula, you have to take the antiderivative of u on the right side of the equation. The goal is always to get a simpler integral on the right side of the equation. So if differentiating u creates a integral more complicated than the original integral on the left, don’t use it.
So we have our answer, the indefinite integral is highlighted. Note, a few principles used in the simplification included reducing the power of the exponent and eliminating the x in the denominator, and bringing out a constant in front of the integral.
Also - in case that wasn't enough (I doubt it), some great videos on integration by parts on YouTube. And if you like cheap books, check out th
e iChapters ad on the right. You can buy individual chapters, in PDF format for a few bucks a piece...that's a cool deal!
![\int_a^b f(x) g'(x)\, dx = \left[ f(x) g(x) \right]_{a}^{b} - \int_a^b f'(x) g(x)\, dx\!](http://upload.wikimedia.org/math/2/d/a/2da4610d98a0ad312b20689afb1bc5d6.png)
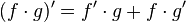



No comments:
Post a Comment