Chebyshev's inequality:In very common language, it means that regardless of the nature of the underlying distribution that defines the random variable (some process in the world), there are guaranteed bounds to what % of observations will lie within K standard deviations of a mean.
So you need the following:
- Mean of the probability distribution
- Standard deviation or variance of the distribution, recall that variance is stdev^2
Let's do a simple example:
The length of a knife is on average 5 inches long, with a standard deviation of 1/10th of 1 inch. What % of observations will be between 4.75 and 5.25 inches long? We can approach this several ways, but let us take the most intuitive route:
The mean is 5 inches...so we're trying to find how often knives will be within 1/4 inch on either side of the mean. Now, if a knife is 5.25 inches, how many standard deviations is the length off by? Recall that our standard deviation is .1 inches. So, .25 inches/.1inch = 2.5 standard deviations. Note that this means that:
mean +/- 2.5 standard deviations = the range of lengths 4.75 to 5.25 inches.
Now we can solve the problem:
So this gives the probability that the observation will be GREATER than k standard deviations. We are trying to find the probability that it's on some interval namely, 4.75 to 5.25 inches. So, if the above is P(A), than the probability we want is 1-P(A).
So let's do it:
1 - 1/k^2 = 1-1/2.5^2 = 1 - 1/6.25 = 1-.16= 84% (.84 = 84%).
So, that's it. Keep in mind this assumes that the MEAN IS KNOWN and the VARIANCE OR STDEV IS KNOWN. If those are not known, you can't use this. And for completeness, what is the probability that the knives observed will be off the 4.75 inch to 5.25 inch interval?
Well, it's just 1-P(that they're on the interval) so 1-84% = 16% OR, and I hope you're thinking about this already, 1/2.5^2 = 1/6.25 = 16%. So that odds that they are either ON or OFF the interval, the union of 2 mutually exclusive events is just their sum, 84%+16% = 100%.
Wikipedia on the subject:
In probability theory, Chebyshev's inequality states that in any data sample or probability distribution, nearly all the values are close to the mean value, and provides a quantitative description of "nearly all" and "close to".
In particular,
* No more than 1/4 of the values are more than 2 standard deviations away from the mean;
* No more than 1/9 are more than 3 standard deviations away;
* No more than 1/25 are more than 5 standard deviations away;
and so on. In general:
* No more than 1/k2 of the values are more than k standard deviations away from the mean.
Let X be a random variable with expected value μ and finite variance σ2. Then for any real number k > 0,
Only the cases k > 1 provide useful information. This can be equivalently stated as
As an example, using k = √2 shows that at least half of the values lie in the interval (μ − √2 σ, μ + √2 σ).
Typically, the theorem will provide rather loose bounds. However, the bounds provided by Chebyshev's inequality cannot, in general (remaining sound for variables of arbitrary distribution), be improved upon. For example, for any k > 1, the following example (where σ = 1/k) meets the bounds exactly.
For this distribution,
A one-tailed variant with k > 0, is
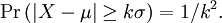



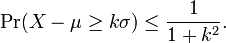

1 comment:
I was searching for this, thanks for the nice tutorial.
Post a Comment